En faisant des recherches sur les lois physiques et mathématiques qui régissent les ondes lumineuses, Duval, l’hebdo de la SAT, a découvert une anecdote sur les ondes sonores qu’il s’empresse de te conter ici.

En 1964, les Beatles viennent de sortir leur dernier single « A Hard Day’s Night ».
C’est le premier accord de la chanson, joué par George Harrison sur sa guitare 12 cordes Rickenbacker qui nous intéresse. Il est reconnaissable entre mille et pourrait presque résumer la musique pop rock des années 60.
Mais un mystère l’entoure : aucun fan n’est encore parvenu à reproduire correctement cet accord !
Comment est-ce possible ?
Un accord n’est pourtant rien d’autre qu’un ensemble de notes. Bref un ensemble de sons, de vibrations qui se propagent dans l’air sous forme d’ondes.
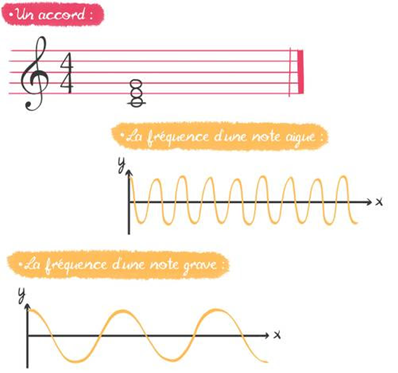
Une note pure correspond, en effet, à une vibration précise, qui se répète un certain nombre de fois par seconde. C’est ce qu’on appelle sa fréquence. Une note aiguë correspond ainsi à une haute fréquence, et une note grave à une basse fréquence.
Pour retranscrire un accord, il suffit de trouver toutes les notes et donc potentiellement toutes les fréquences qui le composent. C’est aussi de cette manière que l’on construit le spectre d’une onde lumineuse.
Et c’est exactement ce qu’a imaginé un fan des Beatles, et accessoirement mathématicien, Jason Brown… Incapable de reproduire le mystérieux accord, il a décidé de prendre le problème à bras le corps.
Et il a utilisé, pour cela, le parfait outil : une opération mathématique appelée “transformée de Fourier“, d’après le mathématicien Joseph Fourier qui l’a mise au point deux siècles plus tôt.
Elle permet de reconnaître les fréquences exactes d’un son. Pratique !
Après quarante ans de mystère, Jason Brown a donc utilisé la transformée de Fourier pour analyser les notes jouées au début de l’enregistrement avec son ordinateur.
Et surprise ! Derrière les guitares et la basse de George, John et Paul se cachait… un piano !
Eh oui, leur manager, George Martin (surnommé le 5e Beatles) a joué, avec le groupe, des notes qui se fondaient dans l’accord.
Indécelables à l’oreille, elles participaient néanmoins à sa magie !
Pour revenir à l’astronomie, sache que la transformée de Fourier est utilisée pour analyser les ondes sonores produites par … Le Soleil !
Si on n’a pas trouvé de partition de piano, on en a déduit l’importance du champ magnétiques solaire dans son chant et décelé la trace de nano-éruptions.